
The aim of this project was to get an understanding of how frequencies in images work and how they can be used in different ways to alter images. For example, magnifying the high frequencies in an image results in a somewhat more sharpened image. Another interesting application of high and low frequencies is the ability to merge images by blurring them at different frequencies and them merging them all together.
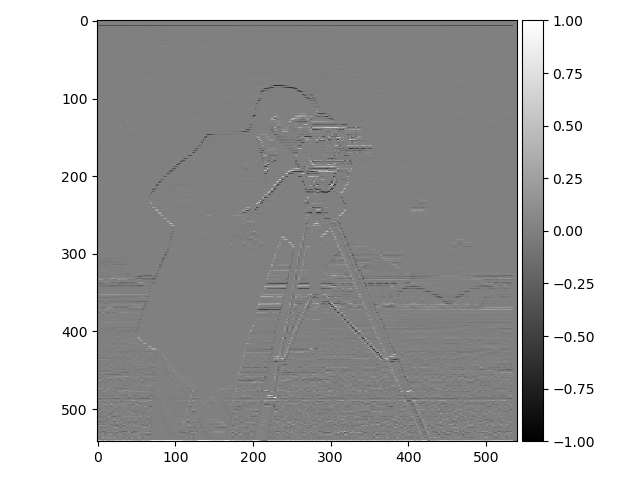
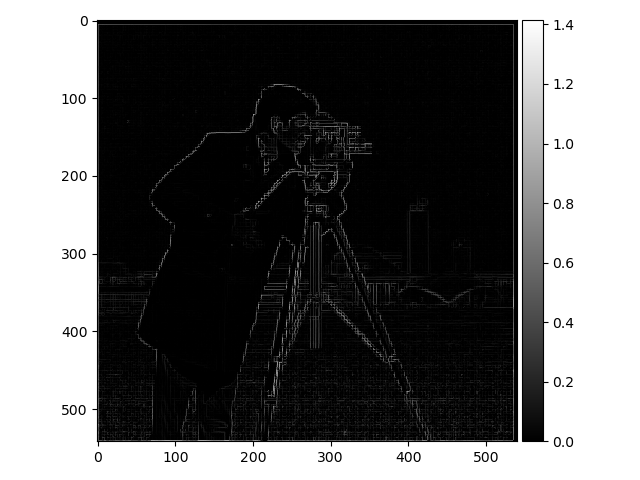
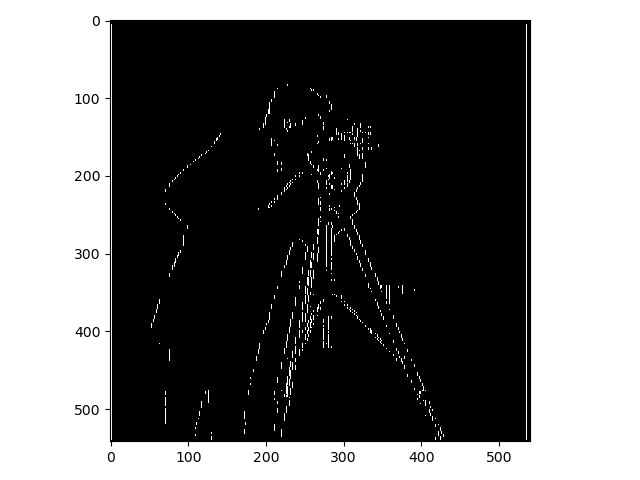
The first task was to show the partial derivatives (gradients: $G_x, G_y$) of an image showing a cameraman. This was done by convoluting the image with finite difference operators: $D_x = \begin{bmatrix} 1 & -1 \end{bmatrix}, D_y = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$ Thereafter these two were combined to show the gradient magnitude. The gradients were also binarized, as in all edges were transformed into a 1 and everything else into a 0, resulting in a black and white image were only the edges were highlighted. The results are presented down below.



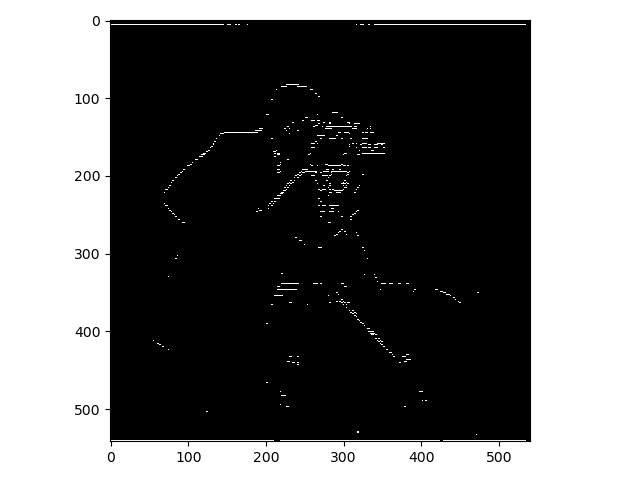
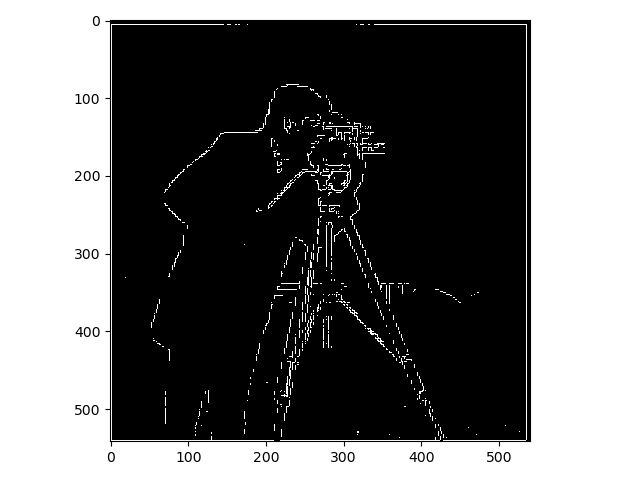
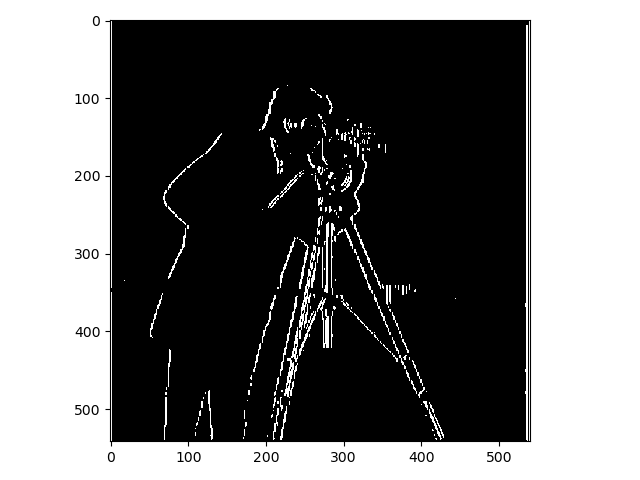
The images above were a bit noisy and to fix this they were smoothed using a Gaussian filter which was constructed Gaussian kernels. The kernels were created using the function cv2.getGaussianKernel() and the images were using a kernel size of 10 and the standard deviation (sigma) was set to 1. After the smoothing the images were transformed in the same way as before. This is clearly a smoother and not as noisy result.



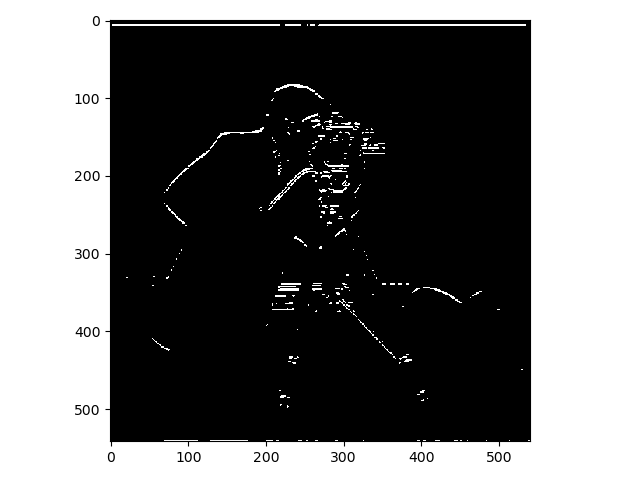
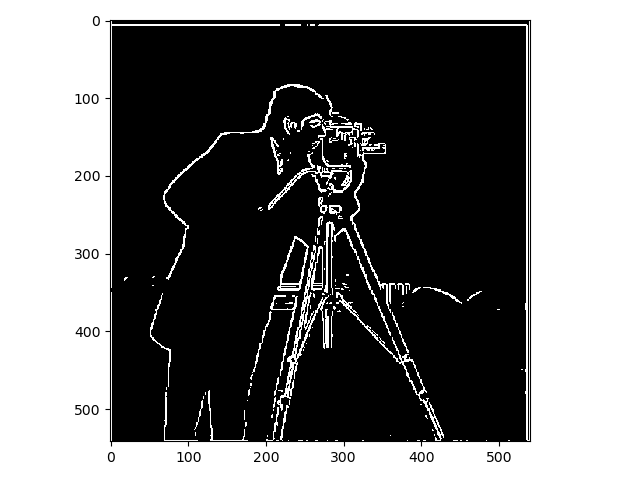
Instead of convoluting the kernels with the gradients of the image the kernels themselves were convoluted with the finite difference operators which results in the derivative of these kernels. The kernels were then convoluted with the original image to compute the partial derivatives of the image and then these were combines in the same way as before. The results displayed below.

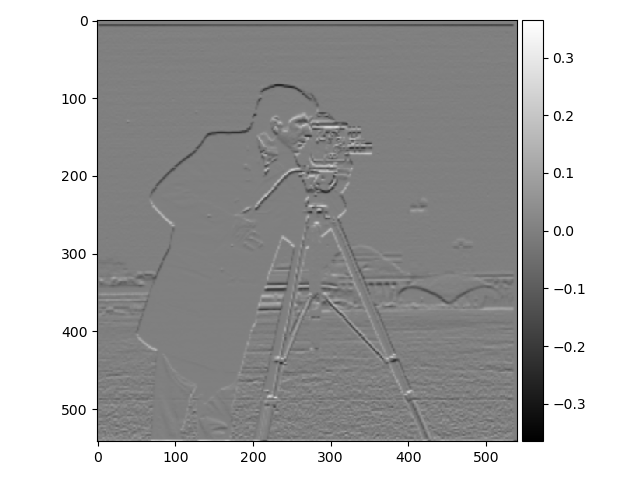

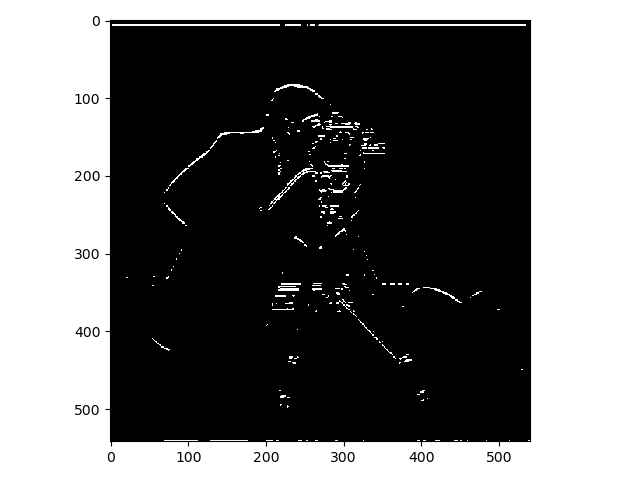
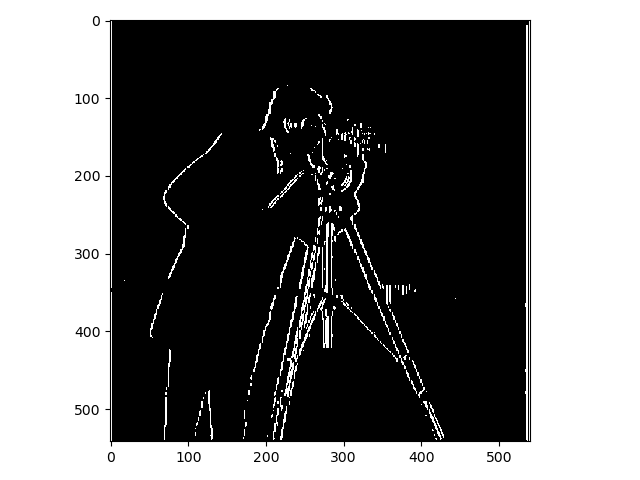
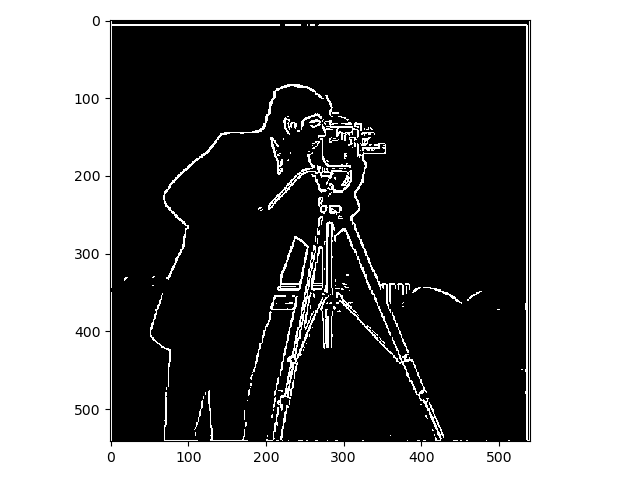
As you can see there is barely any noticeable difference between the two ways of using the Gaussian kernels.
To sharpen images, the original image was filtered using a Gaussian filter were the high frequencies were removed. The difference between this image and the original image is an image inly containing the high frequencies. By adding the original image with the high frequencies, the image can appear to be "sharpened". Two examples of this is displayed below.
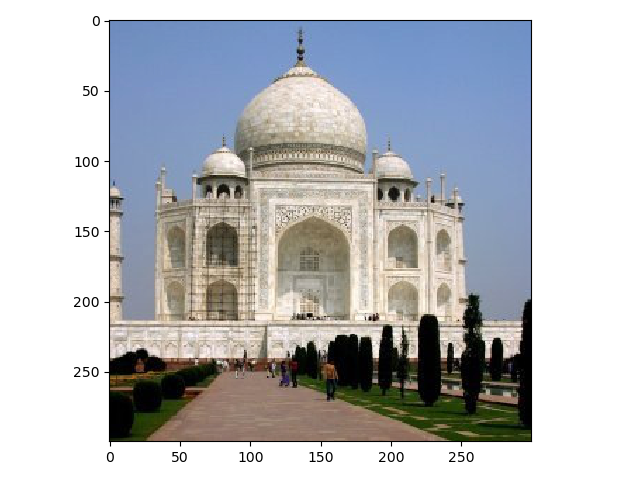
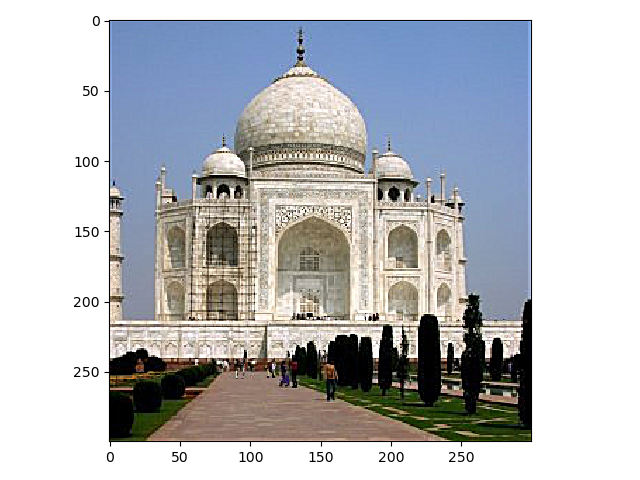
To see how well the sharpening works an image was first blurred and then sharpened. The results are displayed below. As you can see the sharpening doesn't quite do the job since a lot of the high frequencies cannot be retrieved.
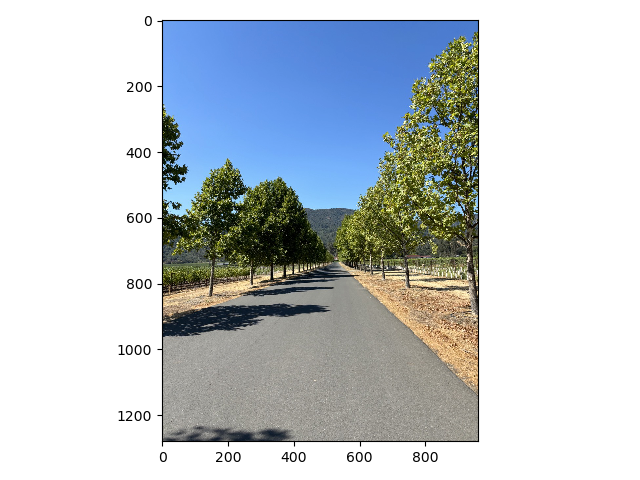
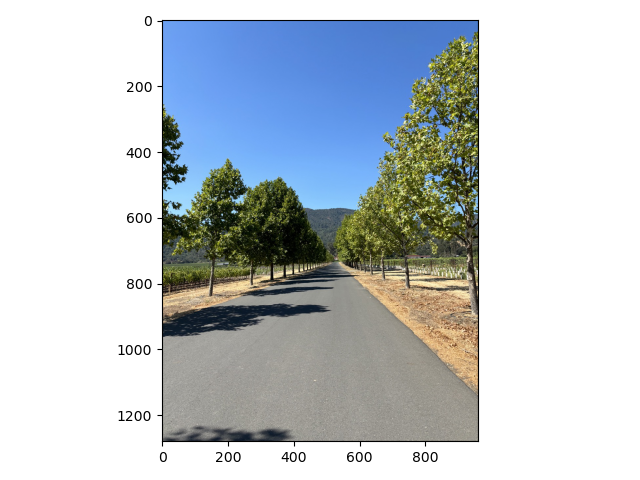
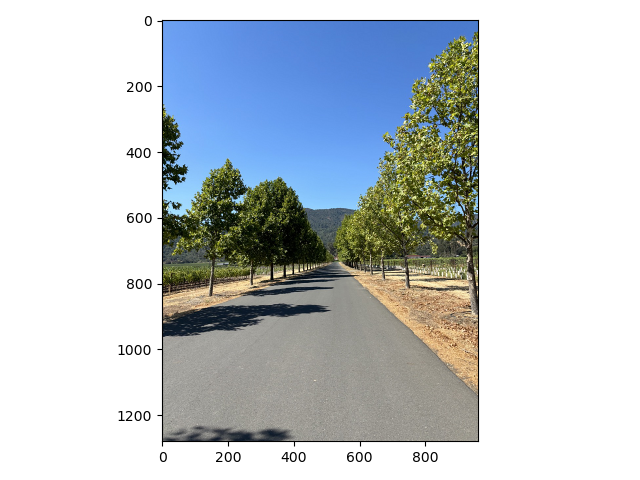
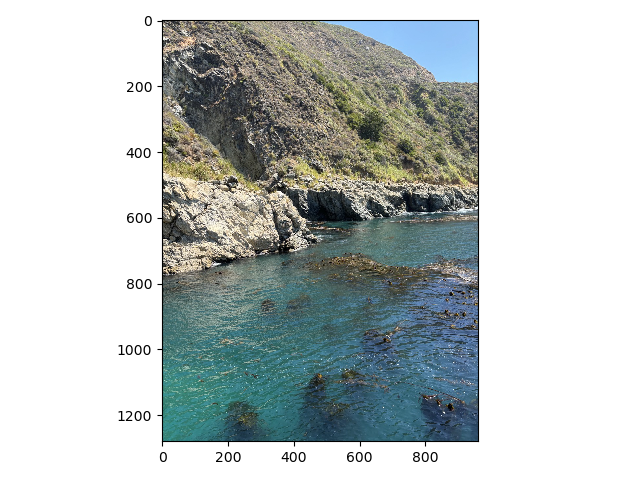
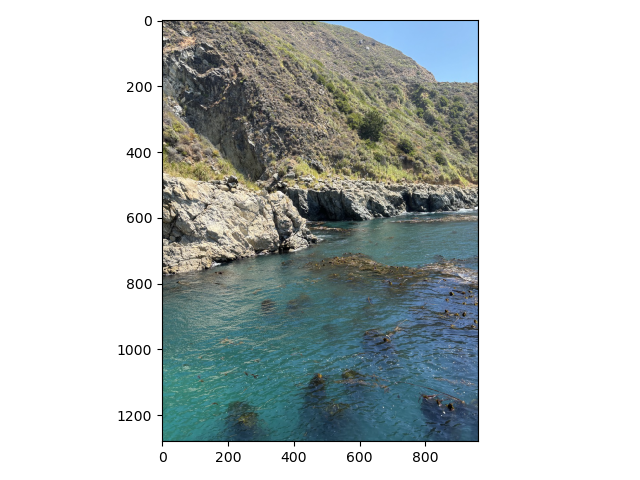
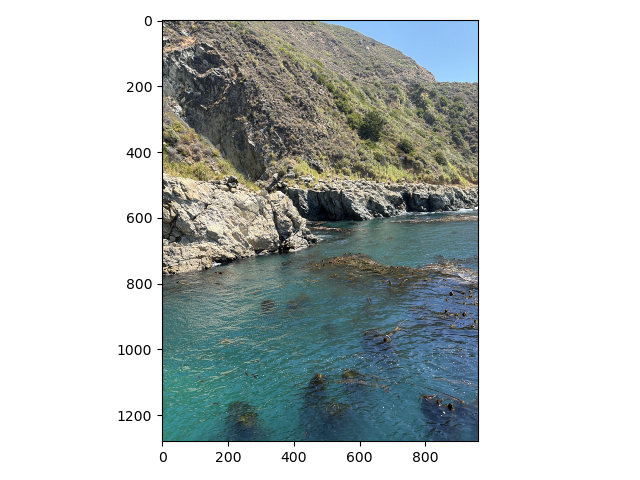
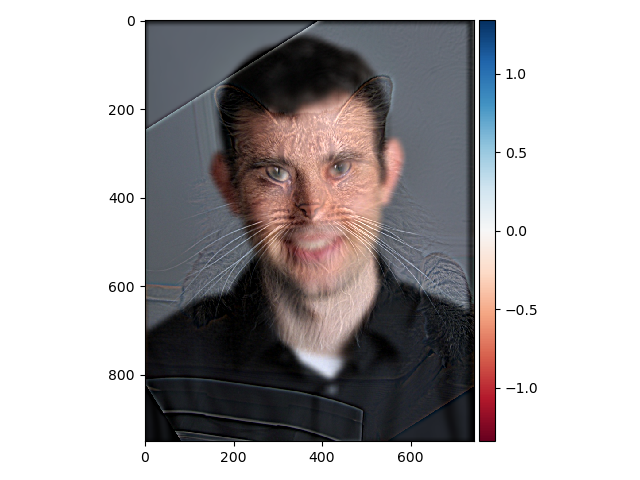
By removing the high frequencies from one image and the low frequencies from another and then laying them on top of each other we can get something called a hybrid image. When you look at the image up close it looks like the high frequency image but when you look at it from far away it looks like the low frequency image. Below are two examples of hybrid images.




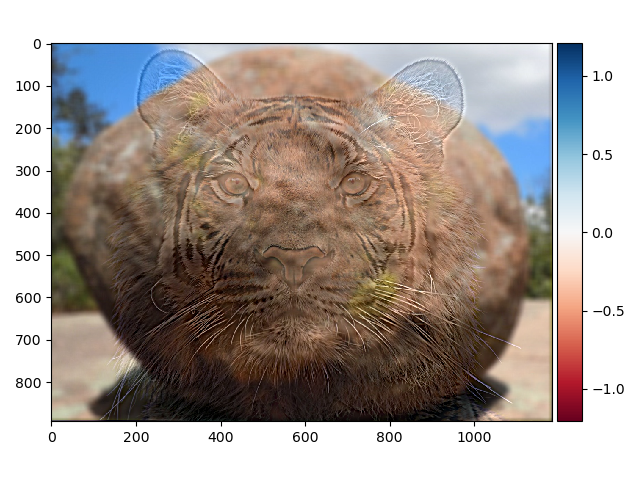
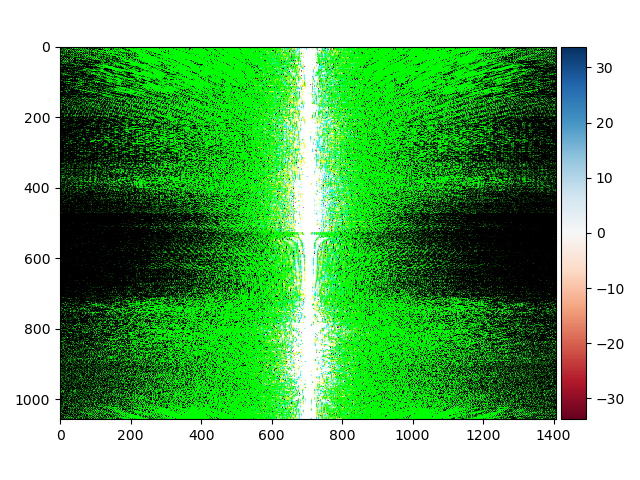
For the image with the cat the fast fourier transform are presented down below.
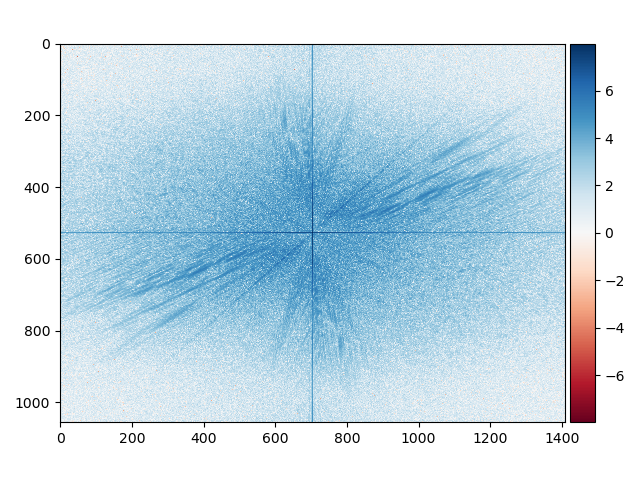
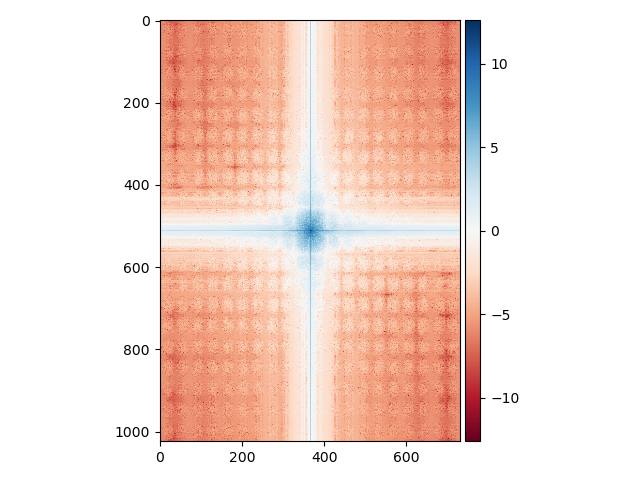
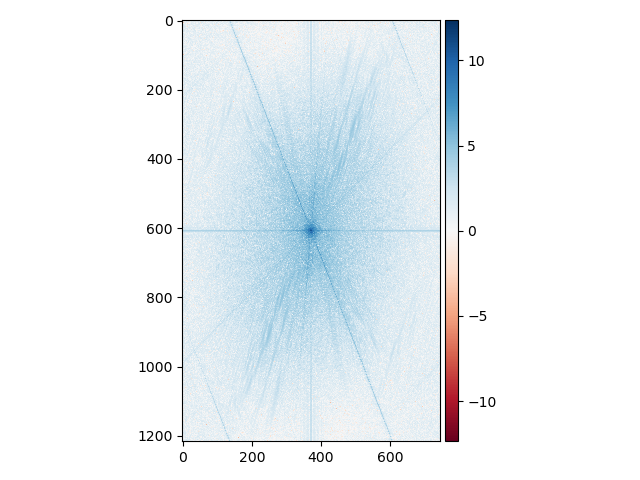
Also the original images using the fast fourier transform are presented down below.
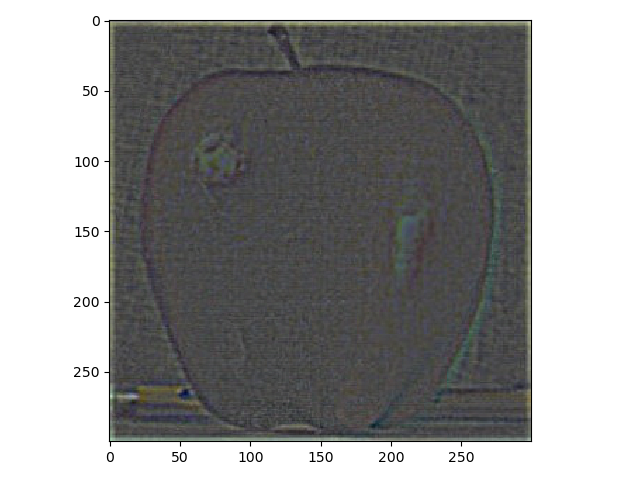
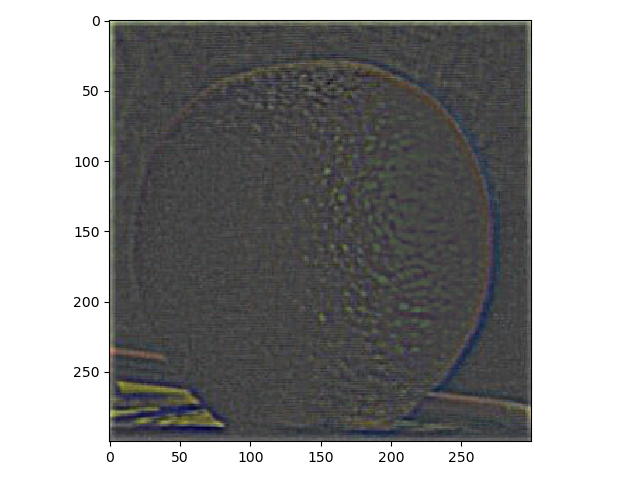
In this part laplacian stacks were made using gaussian stacks. Down below, the result from using a laplacian stack and displaying every level (five were used) on an apple and an orange.
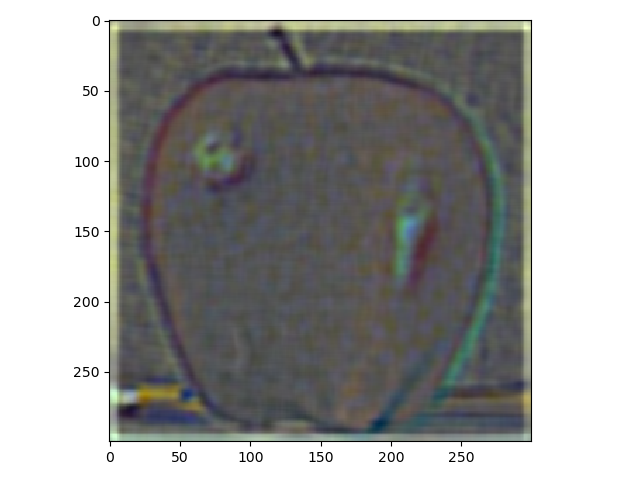
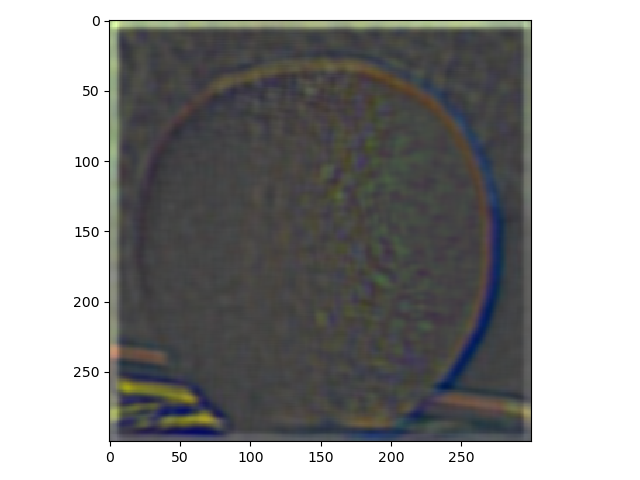
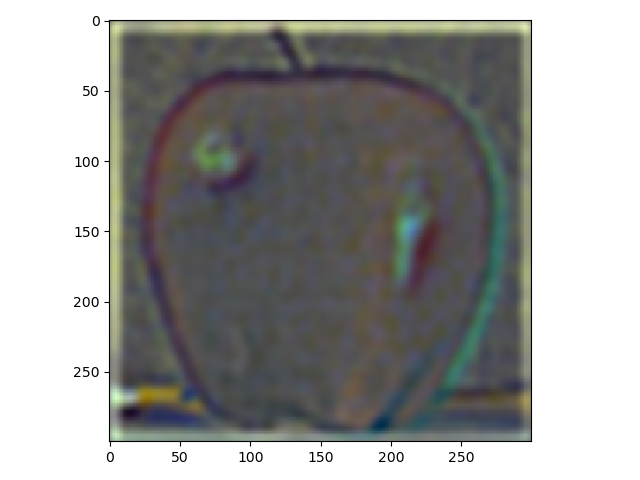
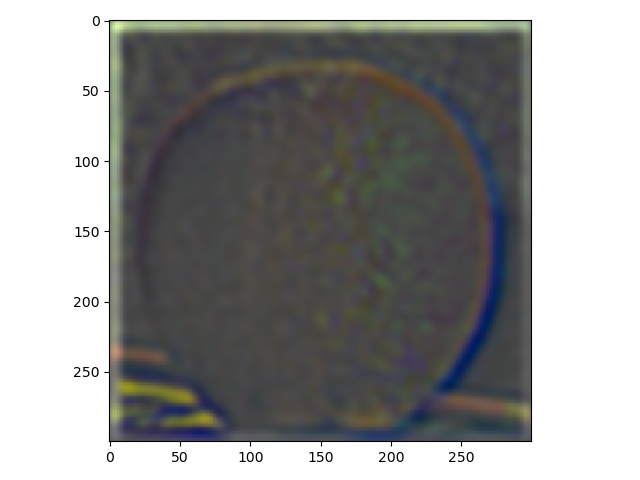
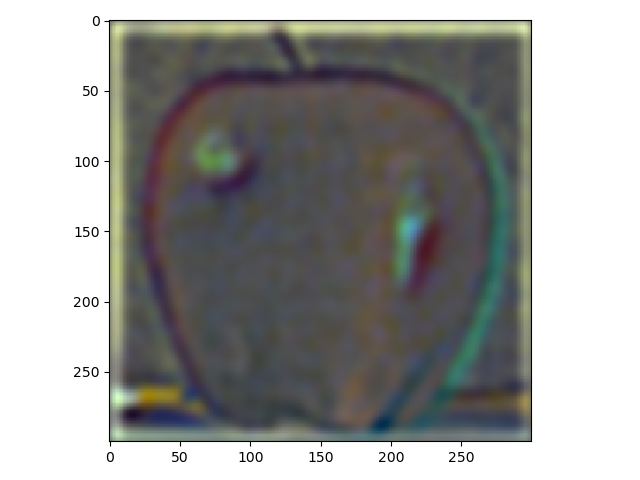
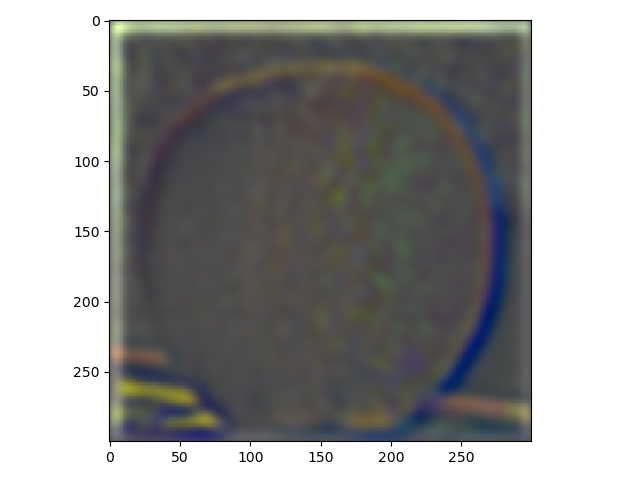
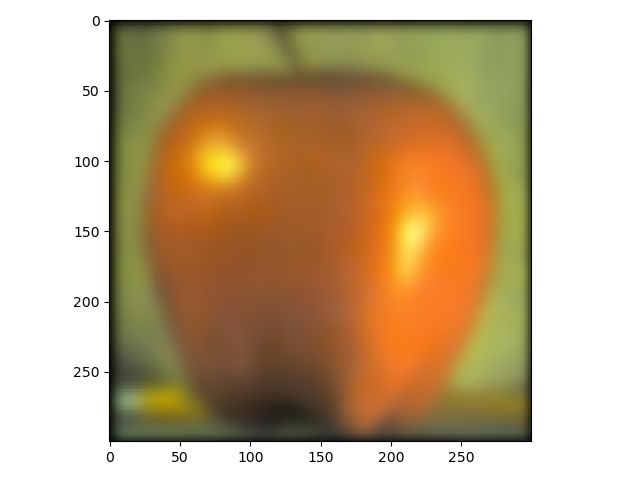
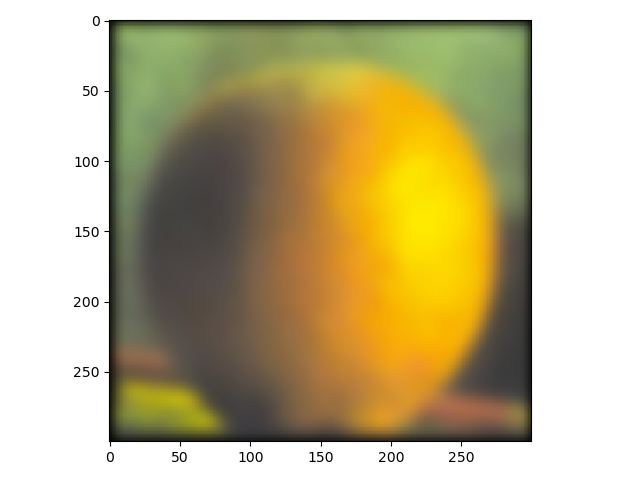
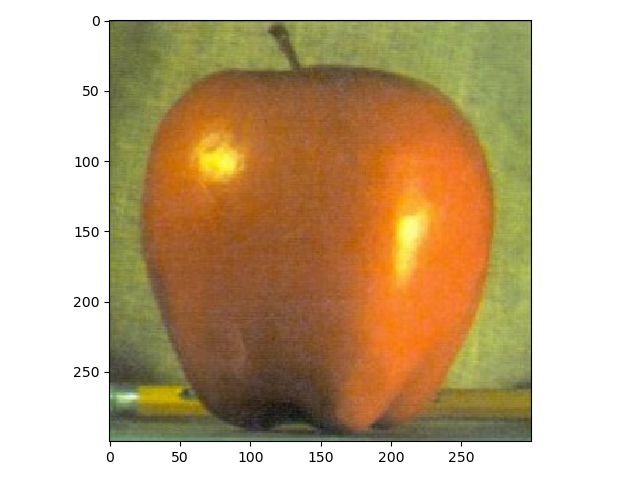
For the last part, the purpose was to blend different images using a mask. The first images which were an apple and an orange are presented down below. The result isn't quite as good as the one shown in the paper by Burt and Adelson but still alright in my opinion.
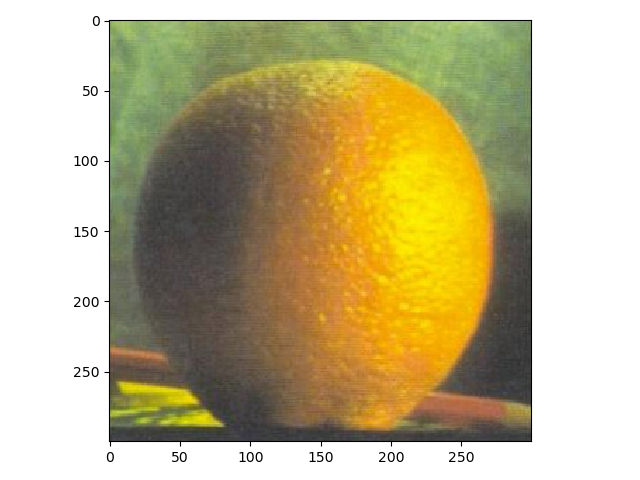
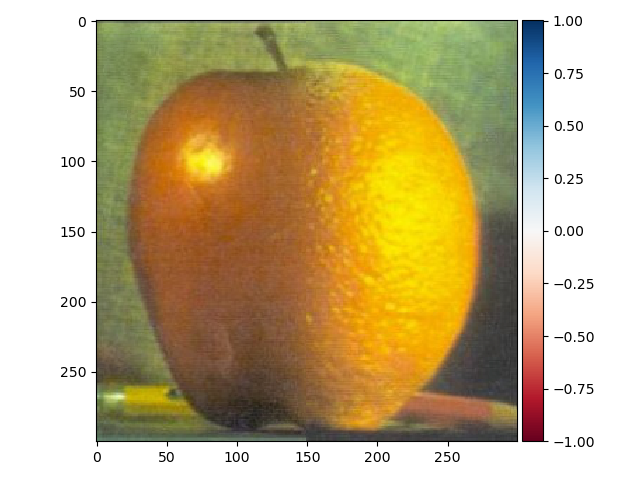
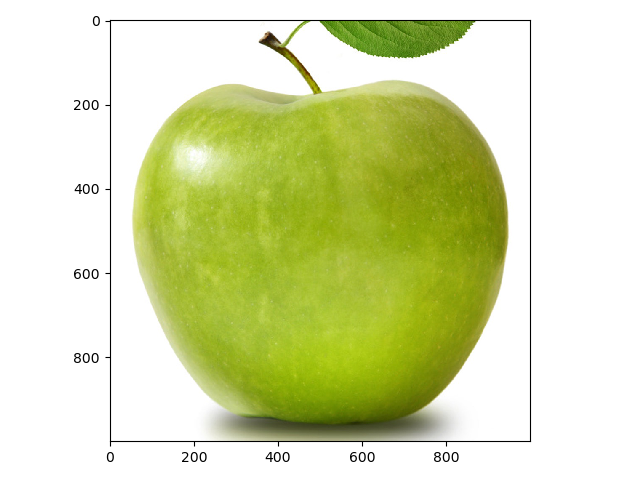
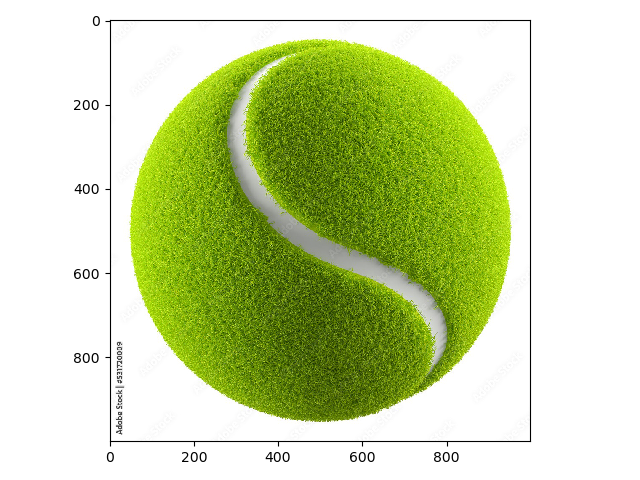
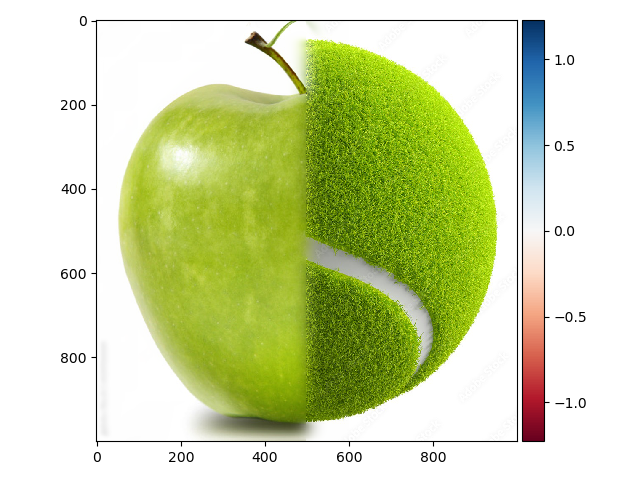
Down below is a failed attempt at blending a green apple and a tennis ball.
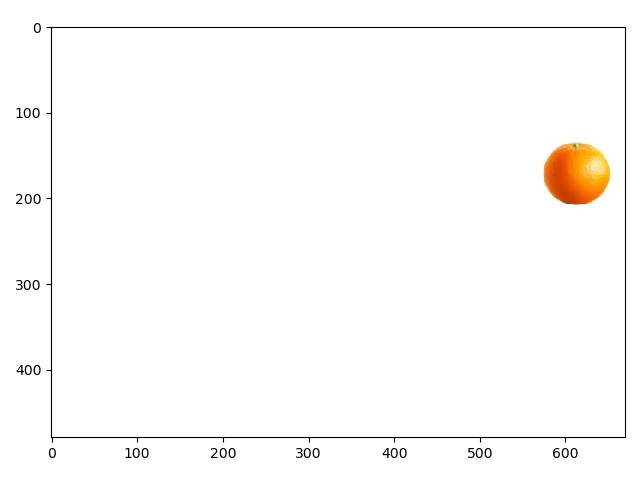
Lastly I used an irregular mask to change the football into a an orange which is displayed below.


All implementations were made with colors.